Jul 23, 19 · Limits of Trigonometry Functions lim┬(𝑥 → 0)sin𝑥 =0 lim┬(𝑥 → 0)cos𝑥 =1 lim┬(𝑥 → 0)〖sin𝑥/𝑥〗=1 lim┬(𝑥 → 0)〖tan𝑥/𝑥〗=1 lim┬(𝑥 → 0)〖(1 − cos𝑥)/𝑥〗=0 lim┬(𝑥 → 0)〖sin^(−1)𝑥/𝑥〗=1 lim┬(𝑥 → 0)〖tan^(−1)𝑥/𝑥〗=1 Limits of Log and Exponential Functions lim┬(𝑥 → 0)〖𝑒^𝑥 〗=1 lim┬(𝑥 → 0)〖(𝑒^𝑥 − 1)/𝑥〗=1 lim┬(𝑥F(x)g(x) = lm quotient rule lim x→a f(x)/g(x) = l/m provided m 6= 0 Squeeze rule for limits If f(x) ≤ g(x) ≤ h(x) for x 6= a, lim x→a f(x) = l and lim x→a h(x) = l, then lim x→a g(x) = l Intuitively, a continuous function is one whose graph does not contain any "jumps" If a function f has a jump at a point a, then we expectLimits Formula What is Limit?

Misc 12 Find Derivative Ax B N Chapter 13 Class 11
Difference between f(a) and lim f(x)
Difference between f(a) and lim f(x)-4) For every x in X, there exists a y in Y such that f (xThen f x L x = →−∞ lim ( ) if for every ε > 0 there is a corresponding number N such that if x < N then ( ) f x L − < ε Definition What this can look like Horizontal Asymptote The line horizontal asymptotey = L is a of the curve y = f(x) if either is true 1 f x L x = →∞ lim ( ) or 2 f x L x = →−∞ lim ( ) Vertical Asymptote The line x = a is a vertical asymptote




Limit Definition Of Derivative Defined W Examples
Definition Latex code Result Limit at plus infinity $\lim_ {x \to \infty} f (x)$ lim x→∞f (x) lim x → ∞ f ( x) Limit at minus infinitySee the Indeterminate Forms wiki for further discussion LetSep 02, 01 · Suppose f is a realvalued function and c is a real numberIntuitively speaking, the expression → = means that f(x) can be made to be as close to L as desired, by making x sufficiently close to c In that case, the above equation can be read as "the limit of f of x, as x approaches c, is L" AugustinLouis Cauchy in 11, followed by Karl Weierstrass, formalized the definition of the limit
If lim ( ) x a f x l → = and lim ( ) x a g x m → =, then lim ( ) ( ) x a f x g x l m → ± = ± lim ( ) ( ) x a f x g x l m → ⋅ = ⋅ ( ) lim x a ( ) f x l → g x m = where m ≠ 0 lim ( ) x a c f x c l → ⋅ = ⋅ 1 1 lim x a→ f x l( ) = where l ≠ 0 Formulas 1 lim 1 n x e →∞ n = ( ) 1 lim 1 n x n e →∞ = 0 sin lim 1 x x → x = 0 tan lim 1 x x → x = 0 cos 1 lim 0 x x → x − = lim 1 n n n x a x a na x a − → − = − 0 1Jan 02, 21 · Let f be a function The derivative function, denoted by f ′, is the function whose domain consists of those values of x such that the following limit exists f ′ (x) = lim h → 0f(x h) − f(x) h A function f(x) is said to be differentiable at a if f ′ (a) exists More generally, a function is said to be differentiable on S if it is2) If x and y are in X, then f (x) = y;
Lim x → a (f(x) ± g(x)) = A ± B = lim x → a f(x) ± lim x → a g(x) As with the product, it is not always possible to use that formula with infinite limits An expression, ∞ ∞ (in the sense of the difference of limits) may happen to evaluate to ∞, a finite number, or ∞ depending on the two limits involvedIn mathematics, a function (or map) f from a set X to a set Y is a rule which assigns to each element x of X a unique element y of Y, the value of f at x, such that the following conditions are met 1) For every x in X there is exactly one y in Y, the value of f at x;Standard Results There are five standard results in limits and they are used as formulas while finding the limits of the functions in which exponential functions are involved ( 1) lim x → a x n − a n x − a = n a n − 1 Learn more ( 2) lim x → 0 e x − 1 x = 1 Learn more ( 3) lim x → 0 a x − 1 x




Formula Continuity And Differentiablity Class 12
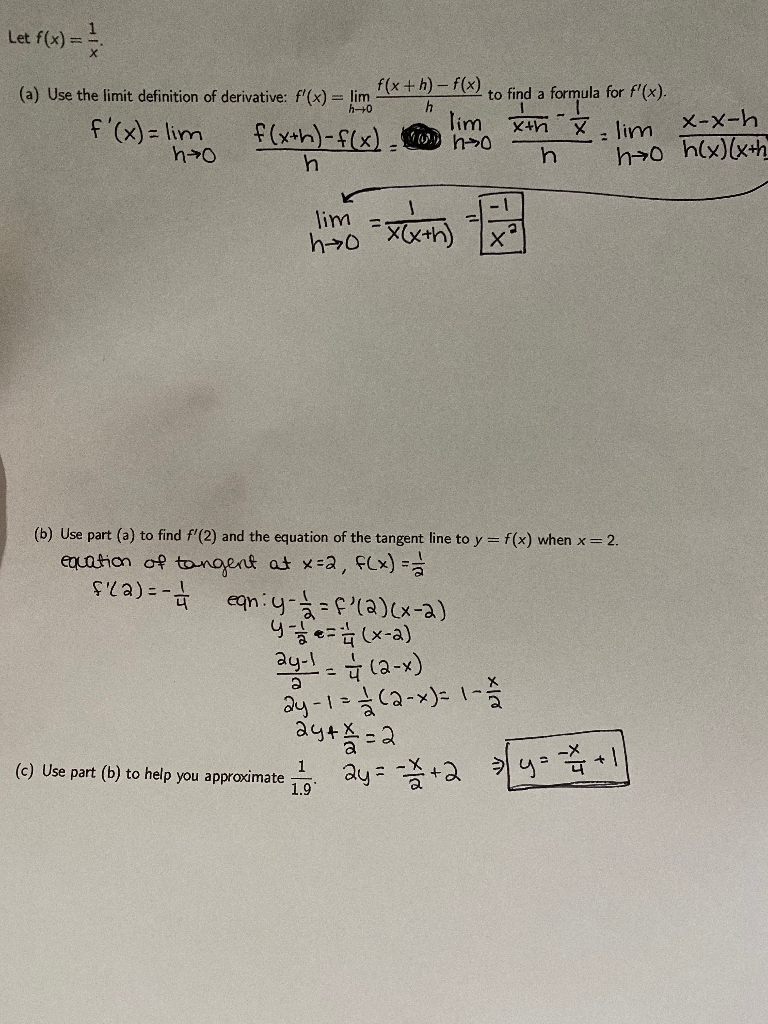



Solved 1 Let C Use Part B To Help You Approximate 1 Chegg Com
May 29, 18 · lim x→af (x) = f (a) lim x → a f (x) = f (a)Nov 22, 19 · For any real number x, the exponential function f with the base a is f (x) = a^x where a>0 and a not equal to zero Below are some of the important limits laws used while dealing with limits of exponential functions For b > 1 lim x → ∞ b x = ∞ \lim_ {x \rightarrow \infty}b^x = \infty limx→∞ bx = ∞,Oct 23, 16 · Explanation lim x→∞ (xe1 x −x) = lim x→∞ x(e1 x − 1) = lim x→∞ e1 x − 1 1 x Direct substitution here produces a 0 0 indeterminate form Apply L'Hopital's rule = lim x→∞ d dx(e1 x − 1) d dx 1 x = lim x→∞ e1 x( − 1 x2) − 1 x2 = lim x→∞ e1 x = e 1 ∞




Derivative Formulas Differential Calculus Derivative




Answered Sketch A Araph Of The Function F X 1 X Bartleby
• Given a formula for the distance traveled by a body in any specified amount of time, find the velocity and acceleration or velocity at any instant, and vice versa 1 12 Functions • limf(g(x)) = f(lim(g(x)),if ∃limg(x)and if f(x)iscontinuousat limg(x)3) If x and y are in X, then f (xMar 24, 17 · Yes, in spite of the fact that mathematics attempts to be precise, ambiguity creeps in Several different types of limits are defined and often we have to infer which type is meant from the context ##lim_{x \rightarrow a} f(x) = L## defines one type of limit when ##L## is a number




Limit Of Function F X And G X From Given Limit Youtube




Given The Function Gx Frac 1 Square Root Of X Fi Gauthmath
(f\\circ\g) f(x) \ln e^{\square} \left(\square\right)^{'} \frac{\partial}{\partial x} \int_{\msquare}^{\msquare} \lim \sum \sin \cos \tan \cot \csc \secF(x) = ˆ x2 sin 1 x if x6= 0 0 if x= 0 The graph of the function shows how the x2 factor squeezes the otherwise wildly oscillating function so that the derivative at the origin is 0 Here is the veri cation f0(0) = lim x!0 x2 sin 1 x 10 x 0 = lim x!0 xsin x = 0 But we can compute the derivative at all other points by the usual formula, and we see that itRemember that the limit definition of the derivative goes like this f '(x) = lim h→0 f (x h) − f (x) h So, for the posted function, we have f '(x) = lim h→0 m(x h) b − mx b h By multiplying out the numerator, = lim h→0 mx mh b − mx −b h By cancelling out mx 's and b 's, = lim h→0 mh h By cancellng out h 's,




If Lim X C F X F C X C Exists Finitely Write The V




Answered Use The Difference Quotient F X Bartleby
Aug 15, 16 · LIM‑1D2 (EK) Suppose we are looking for the limit of the composite function f (g (x)) at x=a This limit would be equal to the value of f (L), where L is the limit of g (x) at x=a, under two conditions First, that the limit of g (x) at x=a exists (and if so, let's say it equals L) Second, that f is continuous at x=LFeb 11, 19 · \(\lim_{x \to a} \frac{f(x)}{g(x)} = \frac{f'(a)}{g'(a)}\), if \(\lim_{x \to a} \frac{f(x)}{g(x)}\) gives the form 0/0 Where, f(a)=0 and g(a)=0 Limits of Exponential and Log Functions \(\lim_{x \to 0} e^{x}=1\) \(\lim_{x \to 0} \frac{e^{x}1}{x}=1\) \(\lim_{x \to \infty } \left ( 1\frac{1}{x} \right )^{x}=e\)According to the composition law, we have $$\lim\limits_{x \to 0}lnf(x) = ln\lim\limits_{x \to 0}f(x) = lnc$$ Because $\lim\limits_{x \to 0}g(x) = d$, we have $$\lim\limits_{x\to 0}g(x)lnf(x) = \lim\limits_{x\to 0}g(x)\cdot\lim\limits_{x \to 0}lnf(x) = dlnc$$ Apply composition lawagain, we get




2 Limits And Derivatives Pdf Free Download




La Debeteca Refuerzo Online Atencion Formula Rapida Para Resolver Facilmente Limites Con Indeterminacion 1 Elevado A Infinito Ver Video Explicativo Youtu Be Bumrpcnj2m Consejos Para Estudiar En Nuestro Instagram
2) If x and y are in X, then f (x) = y;Lim x → c f ( x ) = L {\displaystyle \lim _ {x\to c}f (x)=L} if and only if ∀ ε > 0 ∃ δ > 0 0 < x − c < δ → f ( x ) − L < ε {\displaystyle \forall \varepsilon >0\ \exists \delta >0\ 0F (x)=\ln (x5) f (x)=\frac {1} {x^2} y=\frac {x} {x^26x8} f (x)=\sqrt {x3} f (x)=\cos (2x5) f (x)=\sin (3x) functionscalculator en
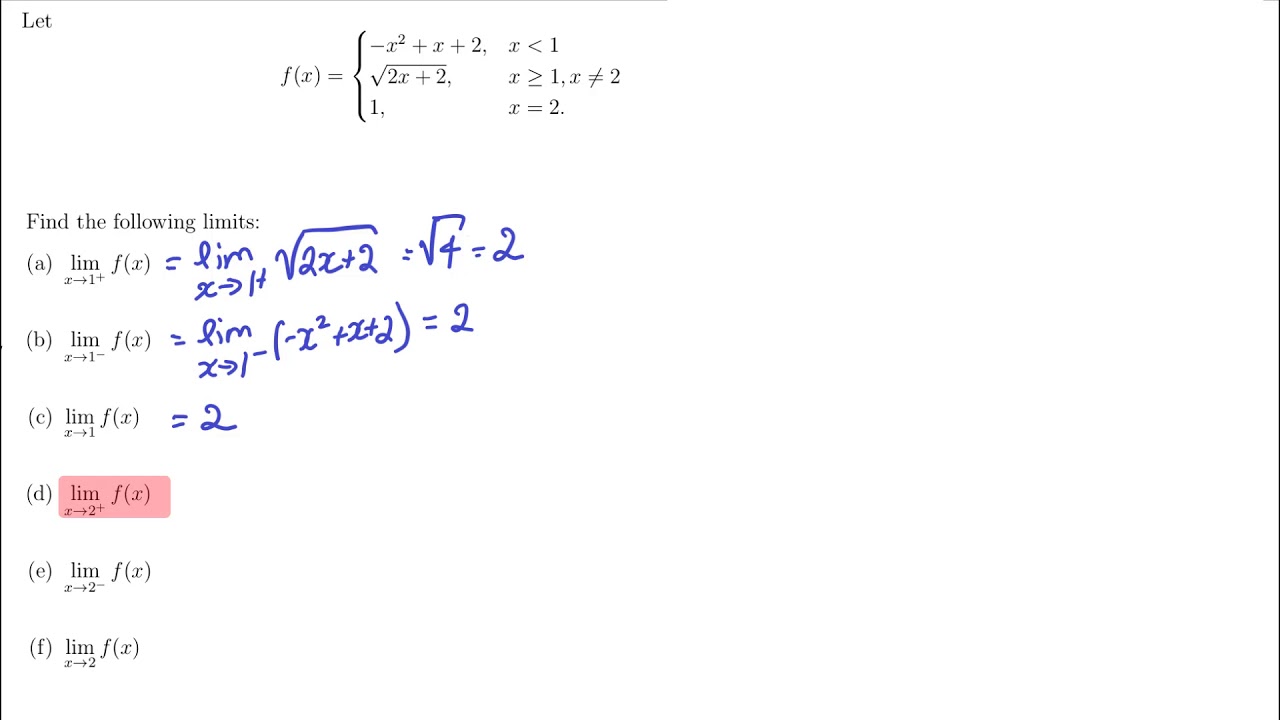



Computing Limits Algebraically




Formula Sheet Of Chapter 5 Continuity Differentiability Class 12 Maths Notes
Please Subscribe here, thank you!!!3) If x and y are in X, then f (x) = f (y) implies x = y;Apr 12, 18 · Intuitive Definition of a Limit Let's first take a closer look at how the function f(x) = (x2 − 4) / (x − 2) behaves around x = 2 in Figure 221 As the values of x approach 2 from either side of 2, the values of y = f(x) approach 4 Mathematically, we say that the limit of f(x) as x approaches 2 is 4




Identify The Formula Of A Rational Function Fx Chegg Com




Ex 7 8 4 Integrate X2 X Dx By Limit As A Sum Ex 7 8
Split the limit using the Sum of Limits Rule on the limit as h h approaches 0 0 lim h → 0 f ( x h) − lim h → 0 f x lim h → 0 h lim h → 0 f ( x h) lim h → 0 f x lim h → 0 h Move the term f f outside of the limit because it is constant with respect to h hLim x → a f (x) g (x) = f (a) g (a) \lim_{x\to a} \frac{f(x)}{g(x)} = \frac{f(a)}{g(a)} x → a lim g (x) f (x) = g (a) f (a) This is an example of continuity, or what is sometimes called limits by substitution Note that g (a) = 0 g(a)=0 g (a) = 0 is a more difficult case;We are given the function, f(x) = 1 x f (x) = 1 x Substitute the given function to the formula of limit definition of derivative




Solved In Each Part Of This Problem The Function F Is De Chegg Com




Formula Sheet Of Chapter 5 Continuity Differentiability Class 12 Maths Notes
F(x) = ∞ c) lim x→−∞ f(x) = 0 d) lim x→0 f(x) = ∞ e) lim x→0− f(x) = −∞ Example Find the limit lim x→−∞ √ 9x6 −x x3 1 Example Evaluate the limit and justify each step by indicating the appropriate properties of limits lim x→−∞ (1−x)(2x) (12x)(2−3x) Solutions Example For the function g whose graph(a) = lim x → af(x) − f(a) x − a We want to show that f(x) is continuous at a by showing that lim x → af(x) = f(a)Aug 16, · Lowercase δ is used when calculating limits The epsilondelta definition of a limit is a precise method of evaluating the limit of a function Epsilon (ε) in calculus terms means a very small, positive number The epsilondelta definition tells us that Where f(x) is a function defined on an interval around x 0, the limit of f(x) as x approaches x 0 is L




Calculus Formulas First Derivative Of A Function F X 0 Gives Critical




Math 150 Formulas
Use any derivative technique to nd the derivative of each function 1 f(x) = 3x4 −x3 4x2 9 Solution f′(x) = 12x3 −3x2 8x 2 f(x) = 4x3 −2x2 4x Solution f′(x) = 12x2 −4x4 3 f(x) = 1 x3 Solution f(x) = x−3 f′(x) = −3·1x−3−1 = −3x−4 = − 3 x4 4 y = 5 √ x Solution y = 5x12 y′ = 5 2x 1 2−1 y′ = 5 2x −1 2 y′ = 5 2·x 1 2 y′ = 5 2· √ xIn mathematics, a function (or map) f from a set X to a set Y is a rule which assigns to each element x of X a unique element y of Y, the value of f at x, such that the following conditions are met 1) For every x in X there is exactly one y in Y, the value of f at x;The number L is called the limit of function f (x) as x → a if and only if, for every ε > 0 there exists δ > 0 such that 0 < x− a < δ This definition is known as ε −δ− or Cauchy definition for limit There's also the Heine definition of the limit of a function, which states that a function f (x) has a limit L at x




Calculus Formulas Limits Integration Trigonometric Functions Complex Analysis




Mate 3 Formulas Integrales Impropias Caso Cuando El Mite Inferior El Superior Ambos Son Infinitos Se Llama Integral Impropia Pueden Ser De Tipos Si Es Studocu
If the existing limit is finite and having its x approaches for f (x) and for the same g (x), then it is the product of the limits A function f (x) usually contains the value of x but it is not compulsory Its best example is if f (x) = (x 4) (x 6)/2 (x 6)Limit Calculator Step 1 Enter the limit you want to find into the editor or submit the example problem The Limit Calculator supports find a limit as x approaches any number including infinity The calculator will use the best method available so try out a lot of different types of problems You can also get a better visual and understandingLimit Definition of the Derivative – HMC Calculus Tutorial Once we know the most basic differentiation formulas and rules, we compute new derivatives using what we already know We rarely think back to where the basic formulas and rules originated The geometric meaning of the derivative f ′ (x) = df(x) dx is the slope of the line tangent




Misc 12 Find Derivative Ax B N Chapter 13 Class 11




Solved If The Tangent Line To Y F X At 3 2 Passes T Chegg Com
Transcribed image text Use the formula f'(x) = lim Z fiz ZX to find the derivative of the function f(x) = Find the second derivative of the function 3 y = 7 (x 7)(x23x) X3 Solve the problem At time t, the position of a body moving along the saxis is m Find the body's acceleration each time the velocity is zeroThe closer we get to 0, the greater the swings in the output values are That is not the behavior of a function with either a lefthand limit or a righthand limit And if there is no lefthand limit or righthand limit, there certainly is no limit to the function f (x) f (x) as x x approaches 0 We writeThe first one is used to evaluate the derivative in the point x = a That is \lim_{x\to a} \frac{f(x) f(a)}{xa} = f'(a) The second is used to evaluate the derivative for all x That is \lim_{h\to 0} \frac{f(xh) f(x)}{h} = f'(x)




Ex 13 1 31 If Function F X Lim X 1 F X 2 X2 1 Pi
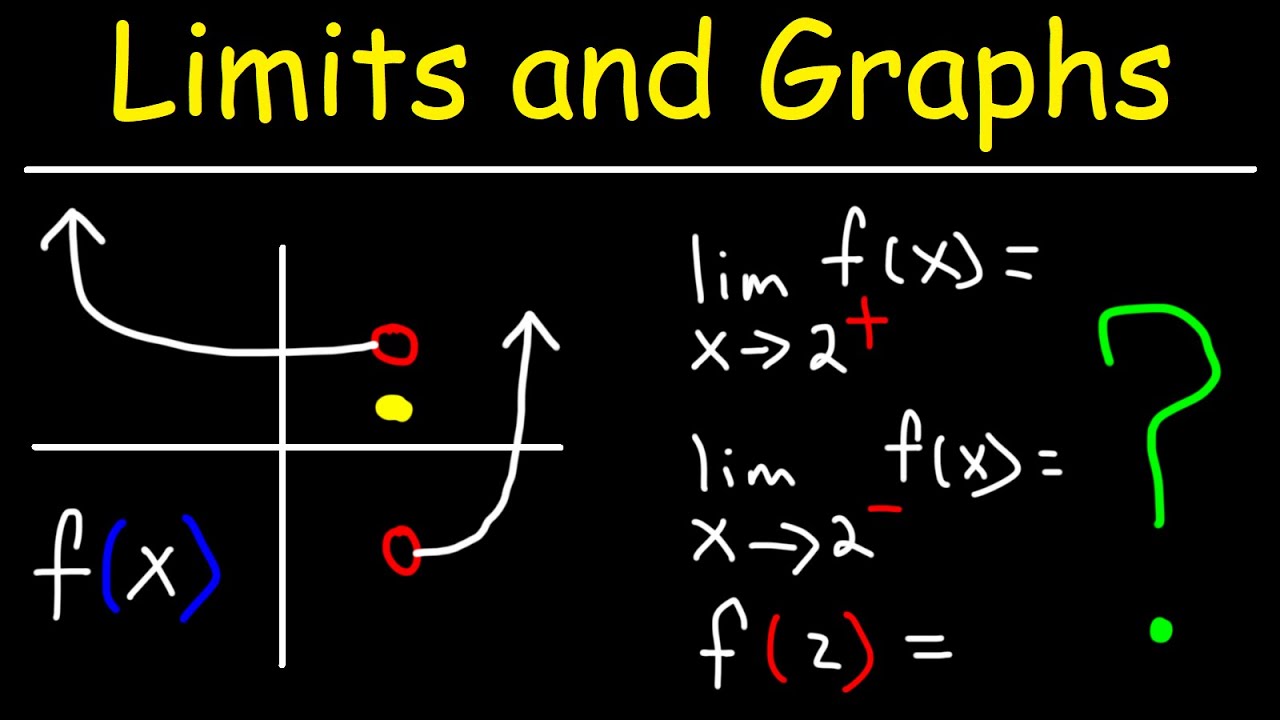



How To Evaluate Limits From A Graph Youtube
Let y = f(x) as a function of x If at a point x = a, f(x) takes indeterminate form, then we can consider the values of the function which is very near to a If these values tend to some definite unique number as x tends to a, then that obtained a unique number is called the limit of f(x) at x = a We can write itLim f(x) = 1 Choose the correct graphJun 03, 21 · Transcribed image text Sketch the graph of a function with the given properties You do not need to find a formula for the function f(1)= 3, lim f(x) = 4 X1 Choose the correct graph below O A B D 10 10 TS х х х 10 10 10 10 10 Sketch a possible graph of a function that satisfies the conditions below f(0) = 1;




Limits At Infinity Infinite Limits And Asymptotes




Limit Laws And Evaluating Limits Owlcation
Dec 05, · Latex limit How to write LateX Limits?Lim f(x) = 2;May 30, 18 · Partial Proof of 1 We will prove lim x → cf(x) g(x) = ∞ here The proof of lim x → cf(x) − g(x) = ∞ is nearly identical and is left to you Let M > 0 then because we know lim x → cf(x) = ∞ there exists a δ1 > 0 such that if 0 < x − c < δ1 we have, f(x) > M − L 1
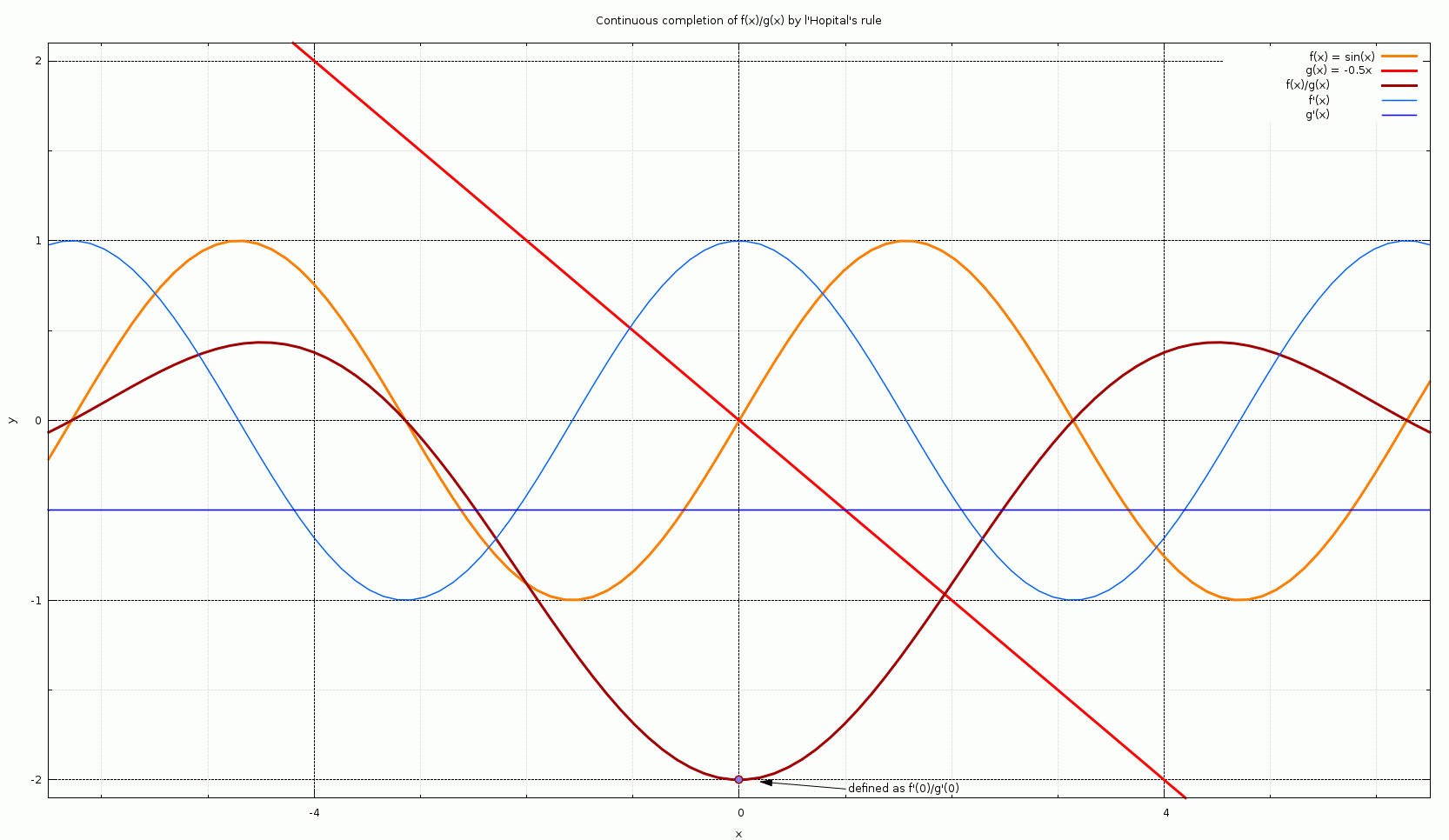



L Hopital S Rule Wikipedia




Calculus I Tutoring Limits Continuity Exercise 2 2 77 To 2 2 84 Www Knowledgemergencies Com
May 03, 15 · At the beginning of the year, in your AP Calculus AB class, you found derivatives by using one of two definitions 1) The derivative of a function at a specific xvalue $\lim_{x\rightarrow a}\frac{f(x)f(a)}{xa}=f'(a)$//googl/JQ8NysHow to Compute the Difference Quotient (f(x h) f(x))/h




Find Formula For A Rational Function With Given Limits Asymptotes And Intercepts Youtube
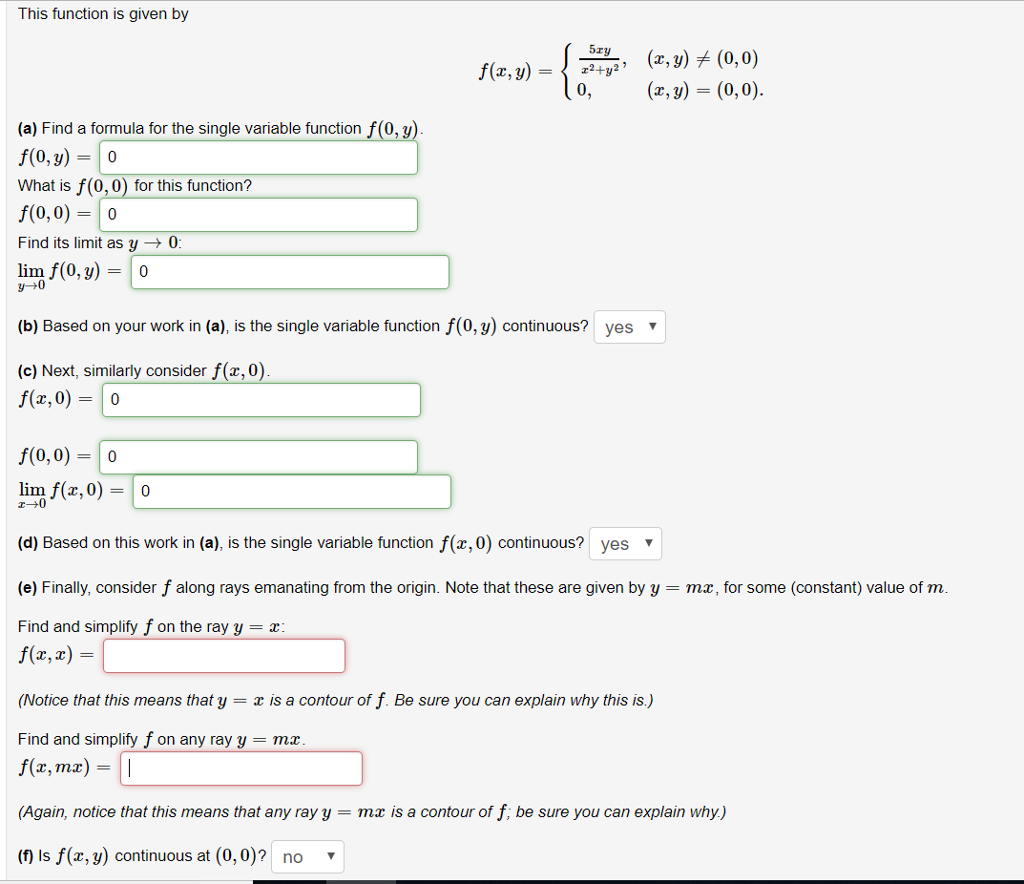



This Function Is Given By 5ry A Find A Formula For Chegg Com




Connecting Limits At Infinity Notation And Graph Video Khan Academy




Formula Sheet For Integration Notes




Rd Sharma Solutions For Class 11 Chapter 30 Derivatives Download Free Pdf Available



Calculus Index Cards




Lim X 0 E X 1 X Formula




Continuity And Ivt




Limit Definition Of Derivative Defined W Examples




Solved 2 Give A Formula For A Function F That Satisfies Chegg Com




Limits By Factoring Video Khan Academy




Definition Of The Derivative Youtube




14 2 Limits And Continuity




Pdf First Order Feynman Kac Formula




Limits And Derivatives Formulas Derivative Mathematical Relations




If Lim X A F X G X 2 And Lim X A F X G X 1 Then Lim




Worked Example Point Where A Function Isn T Continuous Video Khan Academy




How Can I Visualize Lim Limits X Rightarrow Pm Infty F X Lim Limits T Rightarrow 0 Pm F 1 T Mathematics Stack Exchange
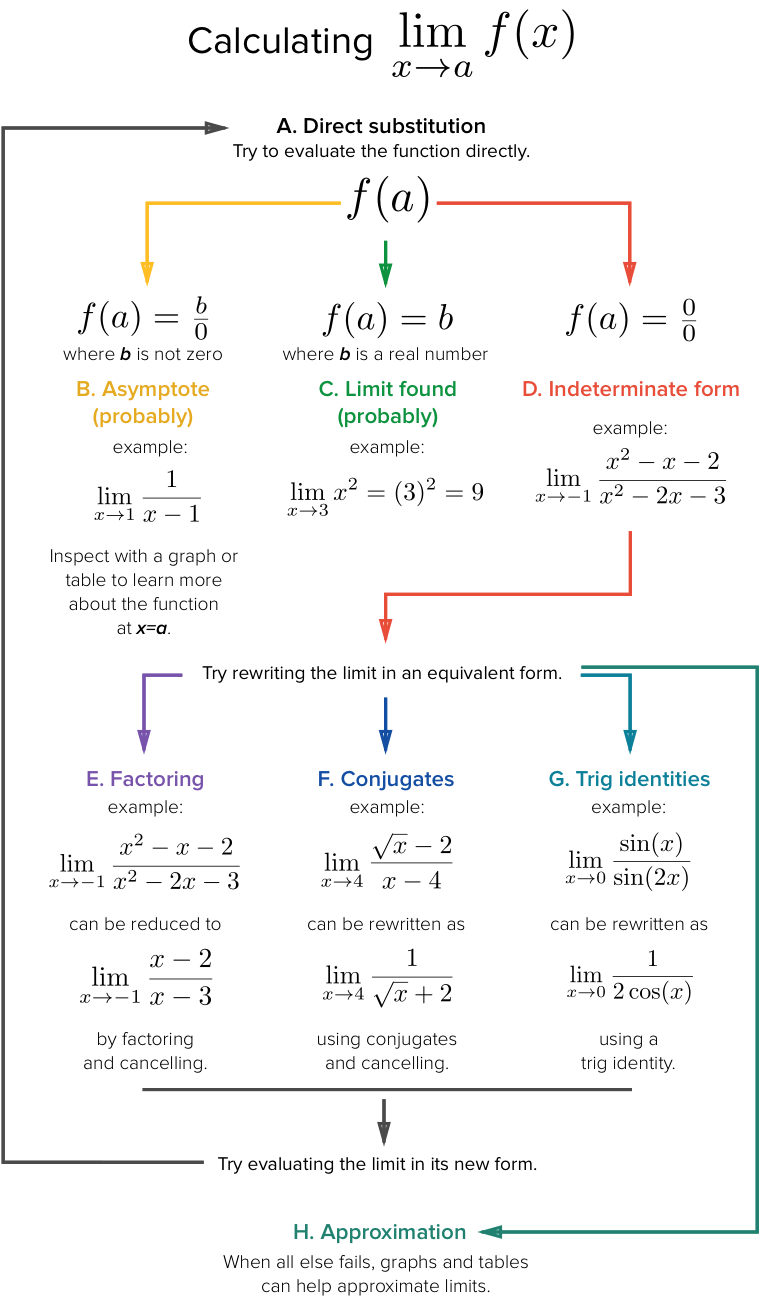



Strategy In Finding Limits Article Khan Academy




Solved Find A Formula For A Function F That Satisfies The Chegg Com




Derivative Of F X 1 X Using The Limit Definition Youtube



How To Compute A Limit With Delta X And A Fraction Difference Quotient And Derivative Of 1 X 3 Youtube




Limits Cheat Sheet Docsity




Limit Limits Limits Calculus I 9 Unsolved Problems Mth 251 Docsity




Continuity At A Point Video Khan Academy




Finite Math 8 2 Notes




25 Questions On Algebra With Applications Quiz 14 Math 141 Docsity
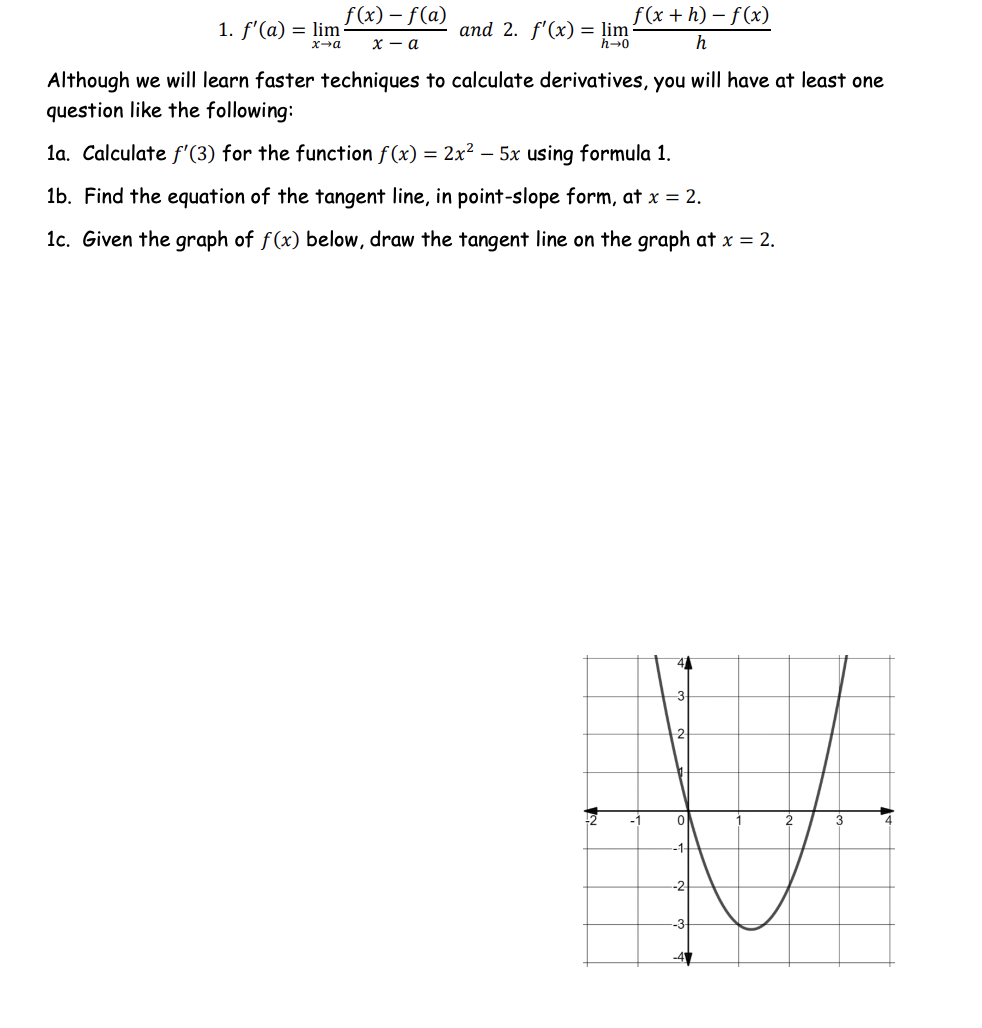



Solved F X F A 1 F A Lim F X H F X And 2 Chegg Com




Answered F Z F X Use The Formula F X Lim Bartleby




Solved X0u W Uive Possible Formulas For F X And G X If Chegg Com




Formula Alternativa Para La Derivada




03 Derivada Usando Definicion Como Limite F X 5x Youtube




0 24 00 A F 0 2 B Lim F X 4 C Lim Chegg Com



Solved 5 Create A Single Function F X Written As A Formula Not Just The Graph That Satisfies All Of The Following Conditions After Making Course Hero




Suppose That A Rational Function Has A Removable D Gauthmath
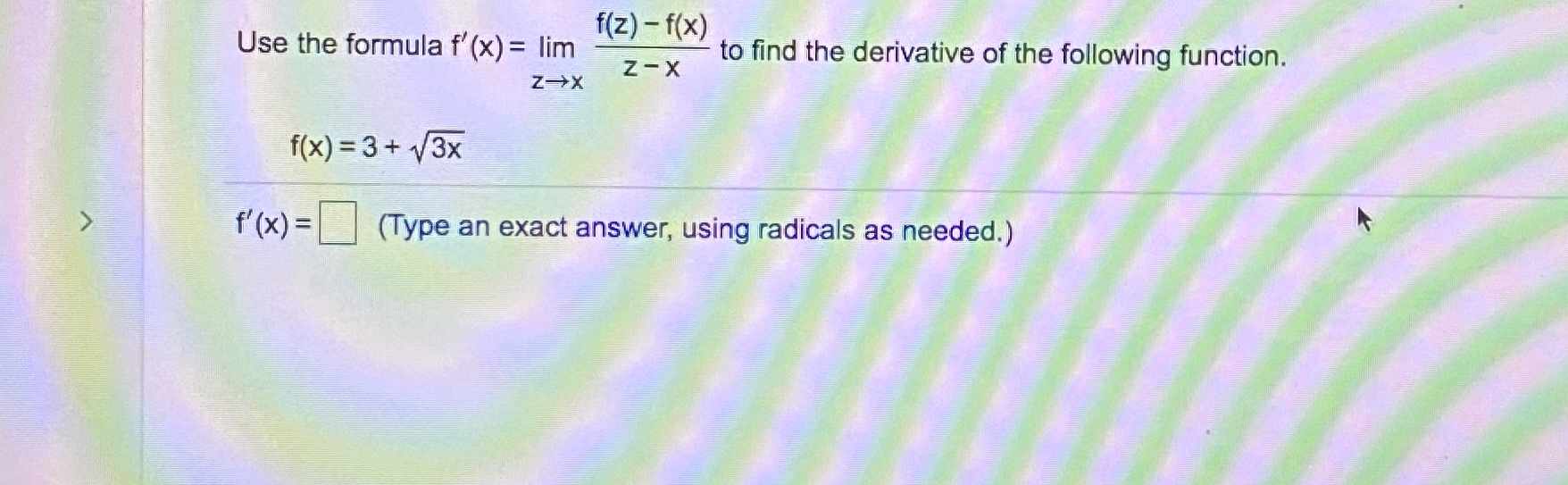



Answered F Z F X Use The Formula F X Lim Bartleby




Answered Formulas Needed F C Ax F C Bartleby




Calculus I Tutoring Limits Continuity Exercise 2 2 63 To 2 2 66 Www Knowledgemergencies Com




1 Definition Of The Derivative Function The Chegg Com




Example 16 Compute Derivative Of Sin X Chapter 13 Class 11




Answered Identify The Formula Of A Rational Bartleby




Ex 13 1 31 If Function F X Lim X 1 F X 2 X2 1 Pi



Evaluate The Limit With Delta X Difference Quotient Youtube




Formulas Limites Matematicas Discretas Ensenanza De Matematica




2 Limits And Derivatives Pdf Free Download




Xi Assign Limits And Derivatives Calculus Teaching Mathematics




Limits Of Combined Functions Video Khan Academy




Bear H S Understanding Calculus



Solved Find The Derivative By Using The Derivative Formula Lim F X 4x F X Ax 0 Ax A Find The Derivative F X 3x2 2x 5 B Find The De Course Hero



Calculus Index Cards




2 Limits And Derivatives Pdf Free Download



Answered Which Of The Following Is A Valid Bartleby




Solved Use The Formula F X Lim 2 X F Z F X Z X To Chegg Com




Solved F Z F X Use The Formula F X Lim To Find Th Chegg Com




Ch 11 Limits And An Introduction To Calculus Ppt Download




Gvvbgm2t Ynwzm




If F X Is Differentiable At X A Find Lim X A X 2f A




Limites Con Fracciones Por La Formula F X H F X H Cuando H 0 Youtube




F Z Fx Use The Formula F X Lim To Find The Chegg Com




Solved F X F A F A H F A 1 Recall That F X Lim Chegg Com
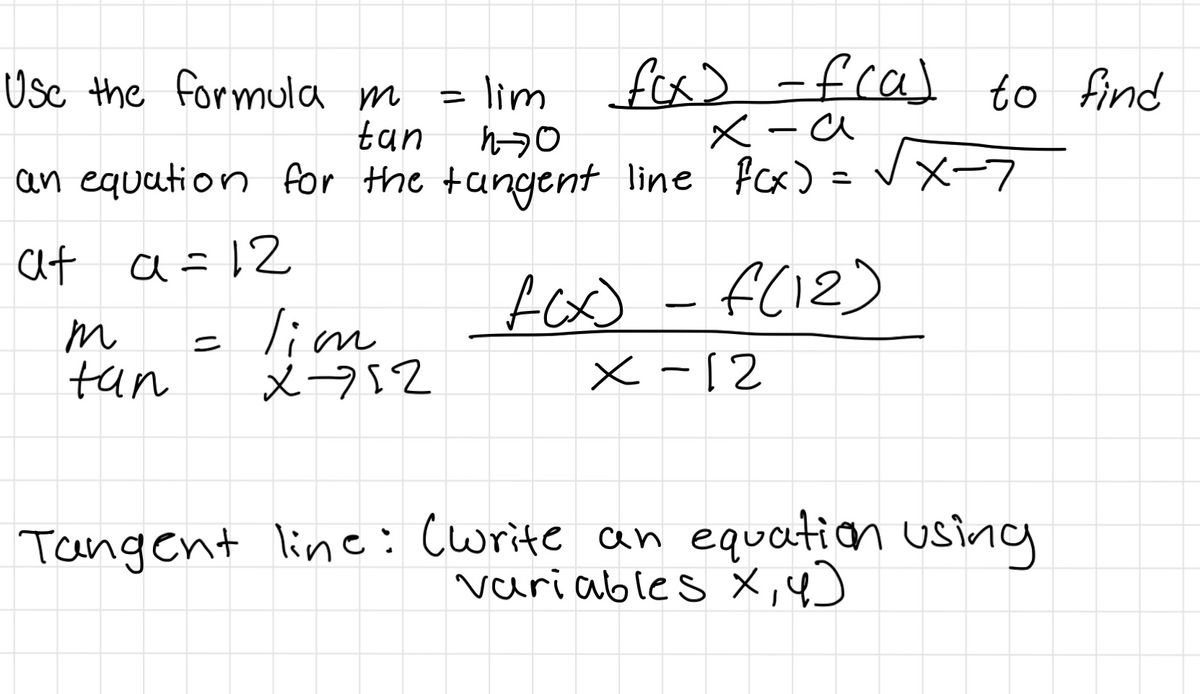



Answered Usc The Formula M Lim Tan Fos Fral Bartleby




2 Limits And Derivatives Pdf Free Download



0 件のコメント:
コメントを投稿